![]()
Из химических институтов приходили ответы, что эта статья биологическая и не по их тематике. Из биологических институтов советовали послать её в химический или медицинский журнал. Медицинские институты отвечали, что статья вообще не медицинская. Никто не хотел вступать на новую и непривычную междисциплинарную территорию.
Почему 37?
(история одной статьи)
Яков Фрейдин

Это в некоторой степени научно-популярный рассказ. Здесь речь пойдёт об одном наблюдении, которое кому-то может показаться интересным, а другим скучным. Поэтому, если около-научные рассуждения вам неинтересны, то бросьте и не читайте.
Много лет назад, в другой жизни, когда я ещё жил в СССР, был у меня замечательный друг Володя Бочков, лет на восемь меня старше. Одно время я даже был его студентом, когда учился в политехническом институте и Бочков вёл у нас курс по электронным приборам. Человек он был энергичный, подвижный, роста невысокого, после окончания института служил в авиации на космодроме Байконур. Там он имел чин лейтенанта, а потому после запуска Гагарина ему прохода не было. Обнимали, качали, автографы брали — ввиду малого роста, воинского звания и возраста принимали за космонавта. В армии схватил он неслабую дозу радиации, из-за чего постоянно мучился проблемами с пищеварением и пытался с ними бороться лечебным голоданием, впрочем, без большого успеха. Может потому судьба отпустила ему малый срок жизни, он умер лишь едва перевалив за 40. До моей эмиграции мы виделись с ним часто. Близкой родни у него не было, жил он один и для моей жены и меня стал как бы членом нашей семьи. Мы его нежно любили — это был добрый, отзывчивый и весёлый человек.

Бочков был невероятно изобретателен и любопытен, его интересовало всё. Особенно всё необычное. Образование у него было инженерное, но любимым предметом была биология. Часто повторял он слова Эйнштейна о том, что «Бог хитёр, но не злонамерен», а потому был уверен, что всё в природе создано красиво, гармонично и по одним и тем же законам. Хотя «Теории Всего» при его жизни не существовало (и сейчас её ещё нет), его острый взгляд всегда подмечал сходство в несхожих вещах. Наподобие Эйнштейна, он старался найти какое-то математическое уравнение, которое бы описывало широкий круг явлений и предметов. Но подход у него был свой — чисто зрительный. Он думал, что сходство внешних форм отражает сходство внутренней сути, а уравнение, которое он искал, как-то должно эту единую суть описывать. Важно для него было, чтобы уравнение это оказалось простым и красивым, ибо в конце концов, Бог не злонамерен, а Миром правят красота и гармония. Бочков всегда носил с собой толстую тетрадь, куда зарисовывал разные графики физических и химических функций, формы органов людей и животных, рисунки и обмеры раковин, рыб — всё, что попадалось ему на глаза и привлекало внимание. Однажды моя мать рассказала, что проезжая в автобусе, увидела в окне на улице промокшего под сильным дождём Бочкова, который стоял у дерева. Потоков воды он не замечал и как ребёнок счастливо смеялся при виде какого-то листочка на ветке, форма которого вероятно подтверждала его теорию о единстве и красоте законов природы.
Идеалом красоты он считал «золотое сечение» или «золотую пропорцию» —число, которое показывает, что размер самой меньшей приметной части объекта или явления относится к его целому размеру примерно, как 0,38. Или наоборот, целое относится к размеру большей части как 1,62. Иными словами, 0,38 и 1,62 это разные способы выразить то же самое отношение.
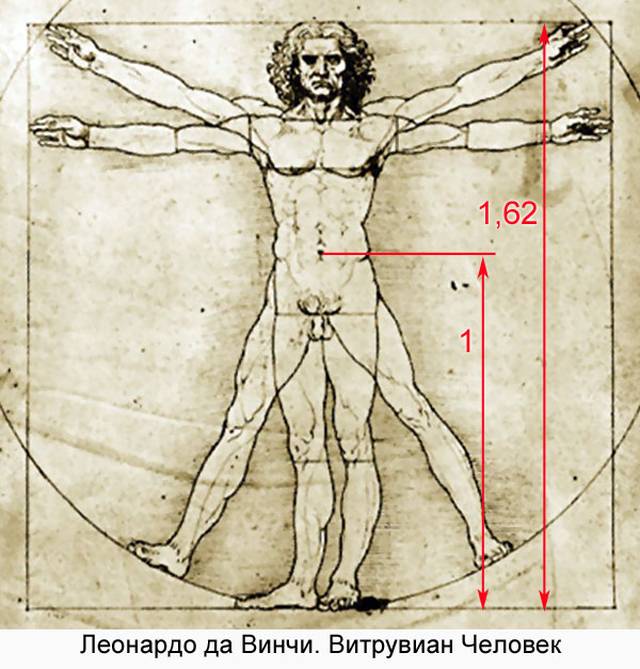
Древне-римский архитектор Витрувиус считал число 1,62 божественным или золотым, так как оно есть отношение роста человека к высоте до пупка. Витрувиус полагал, что всё созданное человеком, должно подчиняться этой пропорции и геометрически соответствовать телу человека — творению богов. Так «золотая пропорция» и стала основой классической архитектуры. Леонардо да Винчи в своём знаменитом рисунке «Витрувиан Человек» изобразил эту пропорцию. Он тоже был поклонником золотого сечения и часто использовал его в своих работах, например в «Моне Лизе». Со времён античности золотое сечение, которое описывает идеальное отношение частей, было найдено в природе в формах многих живых организмов, в спиралях раковин, ураганов и галактик. Художники постоянно его используют в картинах, скульптурах и архитектуре. После 1950, по этой же пропорции в Европе были выбраны размеры киноэкрана, как наиболее удобные для зрения. По какой-то пока непонятной причине для человеческого глаза золотая пропорция наиболее приятна и гармонична. Эта загадка и занимала ум Бочкова — почему?
Естественно, в своих поисках он пришёл к красивому математическому феномену известному, как ряд Фибоначчи, названного в честь математика из Пизы начала 13 века. В этом бесконечном ряду чисел два соседних числа находятся в отношении весьма близком к золотой пропорции, то есть к 1,618 или приблизительно 1,62.
Ряд Фибоначчи это совершенно удивительное явление. Например, возьмите два произвольных числа, скажем, ваш день рождения. Пусть это будет двенадцатое апреля (12 и 4). Сложите их и получите следующее число 16. Теперь сложите два последних числа (4 и 16) и получите 20. Чтобы получить очередное число ряда продолжайте складывать два последних числа и вы получите такую бесконечную последовательность чисел, где каждое число есть сумма двух предыдущих:
12 4 16 20 36 56 92 148 240 388 628 1016 …. и так далее.
Чем дальше вы идёте в этом ряду, тем ближе отношение двух соседних чисел будет приближаться к золотой пропорции. Например, поделите 388 на 240 и вы получите 1,62. Поделите 628 на 388 и вы опять получите 1,62. Неважно с каких чисел вы начали строить ряд и какую пару соседних чисел подéлите, их отношение всегда будет 1,62 — золотая пропорция. Видимо во многих процессах в живой и неживой природе так и происходит: каждая новая часть или ступень есть сумма двух предыдущих частей или ступеней. Что-то такое работает и в нашем мозгу, когда мы воспринимаем внешний мир. Может поэтому золотое сечение в зрительных и слуховых образах как бы идеально соответствует работе мозга, резонирует с ним и потому кажется нам наиболее удобным, приятным и даже красивым? Древние греки и римляне понимали красоту золотого сечения, хотя и не могли это объяснить, а потому списывали всё на волю богов.
Бочков был этим очарован и считал, что примечательный промежуток где-то между 0,36 и 0,38, можно найти в любом природном явлении. Полагал, что уравнение, которое он искал, будет иметь экстремальную точку в районе 0,37 или 37% от шкалы — близкое к золотому сечению 0,38. Мы с ним подолгу беседовали и я обычно играл роль скептика — меня не удовлетворяло только внешнее сходство форм, без понимания внутренней сути. Это казалось мне случайностью и я, в отличие от Бочкова, похожесть внешних форм считал недостаточной для существования какого-то общего принципа. Он огорчался моему неверию и говорил, что когда ни-будь я пойму, что он был прав — форма так просто не возникнет и красота внешняя отражает красоту внутреннюю.
* * *
Однажды, совсем независимо от наших с ним бесед, я решил разобраться с регуляцией тепла в человеческого теле. Мне это было интересно понять по моей работе с медицинскими приборами. Из книг по физиологии я знал как вырабатывается тепло в теле теплокровного животного и как оно регулируется. Непонятно было только почему в здоровом теле человека температура строго держится близко к 37°Ц, а при болезнях повышается? В медицинских книгах это или не объяснялось вовсе или давались какие-то туманные намёки на то, что стабильная температура повышает эффективность биохимических реакций, а жар помогает бороться с инфекцией.
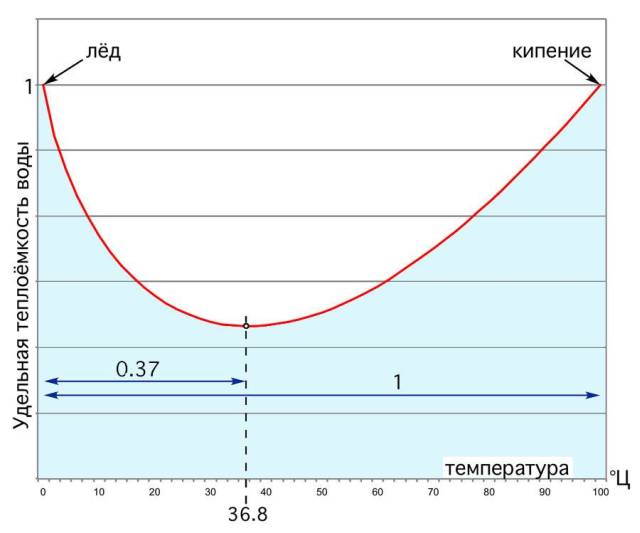
Человек на 60% состоит из воды и поэтому я решил, что в первую очередь надо разобраться с водой. Вода это совершенно уникальное вещество и для её нагрева нужно пропорционально больше энергии, чем для нагрева любого другого материала, то есть у неё самая большая удельная теплоёмкость. Раз так, подумал я, посмотрим как ведёт себя вода при нагревании. Я взял толстый справочник физических величин и к моему удивлению увидел, что теплоёмкость воды есть величина не постоянная, как нас учили в школе, а слегка меняется если воду нагревать от замерзания, то есть от 0°Ц до точки кипения 100°Ц. Удельная теплоёмкость сначала снижается от 1, а потом плавно опять возвращается к единице, когда вода закипает.
Не место в популярном журнале рассуждать о глубоких научных материях, однако для читателей, знакомых с физикой, упомяну лишь, что после долгих размышлений я пришёл к выводу, что удельная теплоёмкость воды должна зависеть от так называемой свободной энергии и описываться формулой энтропии:
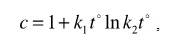
где температура to выражена в градусах Цельсия, а k1 and k2 это постоянные величины. Я построил график по этой формуле, наложил его на данные теплоёмкости воды из справочника и к моему удивлению и радости они совпали совершенно точно. Тут я обратил внимание, что теплоёмкость минимальна в узком промежутке от 36 до 38 градусов Цельсия. Расчёт по формуле даёт точное значение этой температуры минимума: 36.8°Ц или примерно 37°Ц. Тут уж я совершенно оторопел — это ведь и есть идеальная температура нашего тела!
Мало того, я заметил, что на безразмерной шкале эта специальная температура равна 0,37 (принимая точку кипения воды за 1). Я об этом рассказал Бочкову и добавил, что может быть формула энтропии и есть то, что он ищет? Он радостно воскликнул, что про формулу не уверен, но его любимое число 0,37 опять себя проявило причём самым важным для жизни образом!
«А не случайное ли это совпадение?» — спросил я, а Бочков тут же со смехом процитировал Эйнштейна, который говорил, что Бог в кости не играет, то есть Миром правят не случайности. Я же в ответ припомнил комментарий по этому поводу Нильса Бора, который заметил: «Ох уж этот Эйнштейн! Он всегда знает, что хочет Бог». Однако, шутки-шутками, но с этим надо было разобраться — почему именно эта температура 37°Ц идеальна для теплокровных и почему здоровому организму важно поддерживать её с большой точностью и главное — при чём тут теплоёмкость воды?
Первый подход был ясен — теплоёмкость может меняться только если в воде при перемене температуры происходят какие-то молекулярные изменения. Теплоёмкость это лишь внешнее проявление этих изменений, вроде как дым из трубы. Раз дым идёт, значит там хозяева что-то варят, но по дыму ведь не определить, какой будет обед. Надо было выяснять детали. Стал я про воду читать разные научные, популярные и даже спекулятивные статьи. Публикаций оказалось много, но по настоящему серьёзных почти не было. Ну там про тяжёлую воду, что используется в атомных реакторах, литература была, но вот про самую обычную питьевую воду из крана или речки — почти ничего. Но всё же кое-что новое я узнал. Оказалось, что всем знакомое сочетание молекул водорода и кислорода, то есть Н2О, совсем не такое уж простое. Важным оказалось то, что вода не есть однородная аморфная смесь молекул, как мы обычно думаем, а может имеет некоторую структуру. Когда она замёрзшая, то состоит из твёрдых ледяных кристаллов, но вот когда лёд тает эти кристаллы разваливаются и превращаются в жидкость. Однако разваливаются не все. При нагреве вода сохраняет какое-то, хотя и малое, число ледяных кристаллов, которые, как обломки айсберга, в ней плавают даже тогда, когда вода уже совсем тёплая. Оказывается, что такая талая вода очень полезна для растений в животных. Некоторые считают, что миграции китов и птиц на север для вывода потомства объясняются именем тем, что там есть талая вода, благоприятная для вывода особей. А затем весной стаи с молодняком двигаются обратно на юг, поскольку там больше пищи. Но вот если воду доводить до температуры нашего тела не от замерзания, а наоборот — охлаждая от кипения, кристаллов в ней не будет и такая вода куда менее полезна. При кипении все кристаллы разваливаются. Стало быть вода при 37°Ц может быть разной, в зависимости от того кипятили её перед этим или замораживали. От кипячёной и потом охлаждённой пользы мало.
Следующим шагом надо было понять, что за ледяные кристаллы плавают в воде? Я стал искать статьи, где можно было про это прочитать, но на русском языке ничего не нашёл. В одной публикации была ссылка на работу с интригующим названием о кристаллической структуре воды. Автором этой статьи был Нисияма Ивао. Я написал ему в Токио и через месяц он прислал мне оттиск. Статья была короткая, всего три страницы, но на японском языке. Среди моих знакомых никого, кто мог читать по-японски, найти не удалось. Думал сначала, что поможет мой тесть, в молодости проживший в Токио четыре года, но он сказал, что там говорил только по-английски и по-русски, а потому помочь не мог. Выхода у меня не было. Я купил двухтомный японо-русский словарь и принялся за работу. Решил, что если переведу все слова, смогу понять смысл статьи. Это был каторжный труд — в японском языке нет алфавита и найти какой-то иероглиф в словаре невероятно сложно. Для этого надо считать вертикальные и горизонтальные штрихи и затем по таблицам искать подходящий иероглиф и его перевод. Провозился я месяца два, японского языка не выучил, но смысл статьи всё же понял.
Оказывается, что от замерзания до кипения кристаллики воды, в зависимости от температуры, могут иметь пять разных форм, или по-научному, быть в пяти фазовых состояниях. Третья фаза от 30 до 45°Ц и есть диапазон, где теплокровные животные могут существовать. Итак, с водой я разобрался, но вот почему именно 37°Ц, то есть середина этой фазы? И снова я засел за книги и журналы. Интернета в те годы не было и я проводил массу времени в библиотеках. Из работ Лайнуса Полинга, нобелевского лауреата по химии, я узнал, что молекулы воды обволакивают белки, как шуба, и в середине третье фазы при 37°Ц форма водяных кристаллов идеально подходит к формам белковых молекул, что важно для поверхностного сцепления. Белки используют как кристаллы попавшие в кровь с водой, так и те, что формируют из воды сами.
Другие фазовые зоны воды тоже оказались биологически важными. Так середина первой зоны от 0 до 15°Ц наиболее благоприятна для весеннего пробуждения семян, а середина второй зоны от 15 до 30°Ц стимулирует размножение рыб, почвенных бактерий и насекомых. Теперь картина прояснилась и связь между водой и температурой нашего тела стала понятнее. Я поговорил с Бочковым и мы решили — теперь можно об этом написать статью в один из научных журналов.
Поскольку материала набралось много и выводы были логичны, статью я написал. Бочков в этом процессе участия не принимал — его мало интересовали публикации, да и писание не было его сильной стороной. Но поскольку именно его увлечённость золотым сечением подвели меня к уравнению энтропии, как модели теплоёмкости воды, я решил, что в статье авторами должны быть мы оба. Через пару недель всё было написано, иллюстрации готовы и я начал отчаянные попытки опубликовать статью в каком либо подходящем журнале Академии Наук. Однако тут возникла загвоздка. По правилам того времени любая статья в академические журналы должна была быть «представлена» каким ни-будь академиком или членкором. Поэтому я разослал копии рукописи нескольким «светилам» с просьбой дать ей зелёный ход.
Одни не ответили вообще, другие перенаправили рукопись в институты Академии. Из химических институтов приходили ответы, что эта статья биологическая и не по их тематике. Из биологических институтов советовали послать её в химический или медицинский журнал. Медицинские институты отвечали, что статья вообще не медицинская, и так далее. Никто не хотел вступать на новую и непривычную междисциплинарную территорию. Были и ответы от научных жуликов, которые прозрачно намекали, что если мы расширим число соавторов, включив их имена впереди моей и Бочкова фамилий, то шансы на публикацию возрастут. От этого мы категорически отказывались.
Так продолжалось наверное с год до апреля 1976 года, когда я наконец отправил рукопись главному редактору журнала «Экология» академику С.С. Шварцу. Его секретарша позвонила мне через неделю и сказала, что академик приглашает меня на разговор. На следующий же день после звонка я появился в его кабинете. Он встретил меня очень приветливо, всё расспросил — какое у меня образование, чем занимаюсь, почему меня заинтересовала эта тема? Потом он сказал, что наша с Бочковым статья это самая оригинальная и свежая работа, которую он видел за последние годы. Но добавил, что в рукописи есть целый ряд недочётов, связанных в основном с тем, что её писал всё же не биолог и не биохимик, а электронный инженер, да и ряд вопросов остался без ответов. Вот, говорит, возьмите птиц — у них ведь температура не 37, а где-то 40 градусов. Как это объяснить? Тем не менее сказал, что обязательно напечатает статью в своём журнале, но сначала в рукописи надо некоторые вещи изменить, дать объяснение по птицам и другим теплокровным, убрать неточности и исправить формулировки. Сказал, что сам поможет мне привести рукопись в правильный вид. Пригласил меня прийти снова и вызвал в кабинет секретаршу чтобы найти для нашей с ним работы свободное время в его плотном расписании. Ушёл я от него окрылённый — этот чудный человек не только был готов работу опубликовать, но и предложил помочь её отредактировать и, в отличие от некоторых, в соавторы не навязывался.
В тот же день, я позвонил в Таллинн своему знакомому орнитологу Пээту Хорма. Он прикреплял на спины птицам миниатюрные радиопередатчики, отпускал птиц на волю, а потом на расстоянии записывал их температуру в полёте и в гнездах. Пээт обещал прислать мне данные своих опытов. Вскоре я получил от него таблицы, из которых следовало, что в полёте температура тела птицы может доходить до 43°Ц (тепло не успевает быстро рассеиваться), но вот когда птичка спокойно спит в гнезде, её температура опускается до того же оптимума в 37°Ц. Так всё стало на места.
В назначенный день, тёплым майским утром я пришёл в Институт Экологии для встречи с академиком Шварцем. Когда я поднимался на второй этаж к его кабинету, меня поразила какая-то напряжённая обстановка. С угрюмым видом пробегали сотрудники, в коридорах стояли группы людей, о чём-то перешёптывались. Я открыл дверь приёмной и увидел секретаршу в слезах. Ещё не понимая, что тут происходит, я пробормотал, что у меня назначена встреча со Станиславом Семёновичем. Сквозь рыдание она мне ответила, что нынешней ночью академик Шварц умер. Ему было всего 57 лет.
Вместе с ним умерла и надежда опубликовать статью о температуре тела человека.
Бочков со свойственным ему оптимизмом сказал: «Не отчаивайся. Прорвёмся. Чёрт с ней, с Академией, это болото. Давай переделывай статью другими словами, для широкой публики». Мне эта идея понравилась, я рукопись укоротил, убрал специальные термины, переписал всё простым языком и отправил в научно-популярный журнал «Химия и Жизнь», что казался мне наиболее подходящим по теме. И действительно, журнал статью сразу принял, а в редакции какой-то штатный борзописец её ещё лихо обкорнал и «подправил» по своему разумению. Тем не менее, в сентябрьском выпуске журнала за 1976 год ужатая и исковерканная статья вышла под придуманным редакцией заголовком «Тепловой датчик — структура воды», что с моей точки зрения было неверно, но махать кулаками было поздно, да и ненужно. Птичка вылетела из гнезда. Это была моя единственная публикация вместе с моим другом Володей Бочковым.



Мне показалась история про температуру человеческого тела, совпадающую с минимумом теплоемкости воды (или близкую ей), увлекательной; если облечь ее в несколько иную терминологию, то, казалось бы, идея авторов проста и элегантна, на грани с гениальностью (:-); меня она на некоторое время увлекла). Стабильность многих биологических систем (белков, мембран и проч) в значительной степени определяется гидрофобным эффектом, выталкивающим неполярные химические группы (фрагменты) из воды и заставлящим их соединяться и образовывать неполярное микроокружение, чтобы уменьшить контакт с водой (так образуются мицеллы). И наоборот, например, когда белок денатурирует, или мицелла распадается, неполярные группы вынуждены «выглядывать» в воду, что сопровождается потерей энтропии. Именно из-за возможной потери энтропии масло не растворяется в воде. Одна старая интерпретация потери энтропии — «вода вокруг неполярных групп замерзает» (которая восходит к истории «мерцающих кластеров» в воде), а теплоемкость такого перехода положительна. Поэтому, поскольку (!), как изобразил автор, теплоемкость воды самой по себе имеет минимум при 37, можно легко вообразить ситуацию, когда соответствующее изменение теплоемкости неполярной поверхности при денaтурации белка или распаде мембраны, включающее доминирующий вклад «замерзания» воды, становится максимально положительным именно при 37. Это означало бы, что влияние температуры на изменение энтропии было бы максимально в этой точке. При снижении температуры (и положительном изменении теплоемкости) изменение энтропии становится менее положительным. Если …..если изменение энтропии переходит через нулевое значение при 37, эта температура становится точкой максимально положительной свободной энергии фазового перехода (денатурации белка, или плавления мембраны и т.д.). Или, иными словами, это температура максимальной стабильности биологической системы. Построить такую схему просто, но общим явлением это, конечно, быть не может, поскольку требует, например, что для разных белков с одним и тем же (??) числом неполярных остатков и имеющих одну и ту же температуру денатурации, энтропия дентурации всегда была бы одна и та же — такого быть не может. Но, если такое могло бы быть возможно хотя бы для некоторого количества функционально или эволюционно принципиально значимых биологических систем, то … дело в шляпе — это в самом деле, могло бы оказаться изящным обяснением такого совпадения. Не замечательно ли? по-моему, это замечательно. да…….Но, оказывается, минимум в теплоемкости воды — он крошечный — меньше одного процента. То есть график в статье замечательный, но минимум неглубокий. Более того, между 21 и 41 градусами, разница в теплоемкости воды около 0.1%. Поэтому, эта будоражащая воображение теория, по-моему, рушится. Такие крошечные изменения в теплоемкости едва ли могут доминировать и определять стабильность биологичесхих фаз или макромолекул. А жаль…
А как с быть. с положением с золотым сечением и 37 С? Если атмосферное давление снизить в три раза, минимум теплоемкости воды на абсолютной температурной шкале не сдвинется (практически, нет влияние давления), и температура оптимума множества жидкофазных процессов не изменится, по той же причине, но 37 уже не будет соответствовать золотому сечению температурного интервала существования жидкой воды. Так что, вся магия 37 C и золотого сечения становится зависимой от атмоспферного давления?
Короче, вся эта история доставила огромное удовольствие, за что спасибо автору.
Jack Othert — 2016-10-06 09:42:05
====
От вежливости и, тем более, такта Вы не умрёте.
прочитайте замечательные работы Отто Эстерле
Почему жизнь концентрируется при 37°С?
и другие!!!
«..большинство плодотворных идей как раз и возникает на стыке разных наук…» — начало отличное, ещё больше понравилось : «Я не знаю, признают вашу работу научным открытием или нет, но все это очень впечатляет, а цифра 37 действует. магически…»
—————-
На меня, дорогая Инна, магически подействовали статья Якова Фрейдина и ваш комментарий. А также — ком-ий Ю.Н. Хочется поздравить всех : Автора, уваж. Михаила, Ю.Н., Инну Б., собравшихся здесь сегодня, в Мастерской Портала, Евг. Берковича, виновника возникновения этого «сборища» и всю редакцию журнала, за ту магию, которая каким-то таинственным образом соединяет всех нас, от Австралии до Вятки, от можа до можа. Шана Това и метука! Шалом и до новых встреч!
Ну какие мистификации, г-н Ноткин, Яков Фрейдин пишет всегда занятно и весьма правдиво. Занятно — не значит высосано из пальца — обычно его рассказы основаны на реальных фактах, а кажутся мистикой потому, что талантливо закручено. Что же касается числа 37 и то, что про него писал В.Высоцкий и ещё «миллиард», так одно дело удивляться мистике числа (ну, там страшный 1937 год, Пушкин погиб в 37 лет, и т.п.) без каких либо объяснений, и совсем другое — привести гипотезу и попытку её доказать, что автор довольно убедительно сделал. Это две большие разницы. Приведите-ка мне из вашего миллиарда ещё одно такое объяснение.
То, что только «не писал ленивый», так Вы, уважаемый Ноткин, видать тоже ленивый. Я ваши статьи читал а вот про 37 там ничего нет. И напоследок: да, у собак, крыс, слонов и прочих животных температура не точно 37 а может на пару градусов от оптимума уходить, а у пойкилотермных животных (змей, например), она вообще не регулируется, так ведь на то и Дарвинизм существует: недаром человек это венец природы. У нас всё куда лучше оптимизировано. Так что нечему удивляться температурным отклонениям. Жду новых рассказов Фрейдина.
Дорогой Джек, оставим в стороне крыс и змей, но вот ежели у рядового здорового американца, температура тела 98 градусов, Вы что же его и за человека не посчитаете.
Я что-то не пойму, г-н Ноткин, Вы это о чём? 98F это 36.7Ц, то есть всего на 0.1Ц ниже теоретического оптимума. Если Вас эта крохотная разница беспокоит — вот объяснение. В живой природе нет штамповок (исключение — клонирование) это Вам не «Хайтек», особи даже одного типа на молекулярном уровне разные. У всех людей белки чуть отличаются, как отпечатки пальцев, а стало быть для них реакция гидратации, то есть сцепление с кристаллами воды, тоже чуть разная. Поэтому у всех людей температура не точно одна и та же, а может быть выше-ниже идеальной с вариациями до 0.8Ц. Так что успокою Вас — большинство американцев — люди, по крайней мере с биологической точки зрения.
Вы пишете: «98F это 36.7Ц, то есть всего на 0.1Ц ниже теоретического оптимума.»
Не ниже, а выше. Оптимум 36,6Ц.
Г-н Othert, право не думал, что придется настолько разжевывать мою мысль. Она заключается в том, что измерять температуру тела человека или другого теплокровного по шкале Фаренгейта или любой другой температурной шкале столь же правомерно, как и по шкале Цельсия, но при этом исчезает всякая связь с числом 37, которому посвящена первая половина статьи. Десятые доли градуса и «оптимум» здесь естественно не при чем. Все шкалы условны и относительны. Кстати сам Цельсий предложил принять за ноль точку кипения воды, а температуру плавления льда считать равной 100 градусам. «Переворачивали» его шкалу другие. Изучение физической величины- температуры, а также термодинамики, энтропии имеет долгую историю. Предметы эти не простые, но я не сторонник ни упрощать их, ни усматривать в них нечто сверхъестественное. Ваше право придерживаться иного мнения. Если не возражаете, давайте на этом закончим.
Да, разжёвывать надо сильнее, чтобы понять, что нет ни малейшей связи со шкалой измерения и законами природы. В науке куда правильнее пользоваться безразмерными шкалами, то есть в нашем случае от 0 до 1 (см. график в статье — так указаны 0 и 1 в безразмерной шкале). Поясню: в шкале Фаренгейта математически оптимальная температура по формуле из статьи Фрейдина равна 98.2F (36.8Ц), тогда как вода существует от 32F до 212F (212-32=180F — вся шкала в F). В этой шкале 98.2 находится как раз в точке 37% от начала до максимума. То есть 37 никуда не исчезает, просто надо правильно на это смотреть. Поэтому неважно какая шкала: Цельсий, Фаренгейт, Реомюр, и т.д., независимо, как мы это измеряем — 37% никуда не исчезает. Никакой ошибки у автора нет, надеюсь, что Вы теперь с этим согласитесь. И напоследок, чтобы действительно закончить эту дискуссию: хотя теоретически оптимальная температуре 36.8Ц (по формуле), средняя температура у людей зависит от места измерения: подмышкой она 36.6, в прямой кишке она 37.3, и т.д.. Идеальная — скорее всего в гипоталамусе (центр мозга), но туда живому здоровому пациенту ещё никто не забирался, чтобы измерить. Желаю всего доброго и теперь действительно закончим.
Не только у птиц, но и у собак температура тела выше 37°Ц — 38.5°Ц, а также у кролика, крысы и т.д.
Яков Фрейдин – большой мастер розыгрыша. Только этим можно объяснить его «вброс» в Мастерскую историю о числе 37 под соусом научного открытия. В ней однозначно достоверно существование в ХХ веке эколога и зоолога академика Шварца. Что же касается самогó простого числа 37, о котором писал еще В.Высоцкий, то о его действительно поразительной распространенности в природе и человеческой жизни, не писал только ленивый. В Интернете число публикаций о нем зашкаливает за миллиард, что наверняка известно уважаемому Архивариусу. Это ,конечно, не снижает занимательности историй Я.Фрейдина.
Здесь речь пойдёт об одном наблюдении, которое кому-то может показаться интересным, а другим скучным.
_______________________________________________
Я бы сказала, что наоборот, это читается как детективная история.
Не знаю, кто сказал, что природа не так расточительна, имея в виду, видимо, связь всего сущего на Земле и во Вселенной. И настоящий ученый должен «находить закономерную общность в самых далеко отстающих фактах, разбросанных по жизненному полю без всяких, казалось бы, связей и толков. Этот толк, эти связи он обязан найти» (О.Фрейденберг).
И это хорошо понимали другие выдающиеся ученые. Злоупотреблю еще одной цитатой, поскольку эта тема очень злободневна и болезненна даже.
« Если я к чему-либо более способен, чем огромное большинство людей, то это к соединению вещей, рассматриваемых обыкновенно в отдельности, сочетанию разных сторон и раскрытию единства в разнообразии явлений», так скромно писал о себе В. фон Гумбольдт, классик теоретического языкознания.
Естественно, что «никто не хотел вступать на новую и непривычную междисциплинарную территорию», отклоняя вашу статью. Для этого нужен другой научный горизонт. Ведь большинство плодотворных идей как раз и возникает на стыке разных наук.
Я не знаю, признают вашу работу научным открытием или нет, но все это очень впечатляет, а цифра 37 действует. магически.
Заодно и АРХИВАРИУСУ. Предлагаю внести кандидатуру ЯКОВА ФРЕЙДИНА за вклад в науку в номинацию «НАУКА».